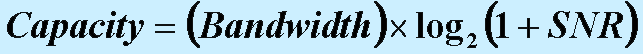 |
A Bit About Shannon's Equation
| Background. If we know the bandwidth of a channel we should be able to figure out its capacity. But the formula for doing this depends on how well the signal is transmitted. The relationship that Claude Shannon developed in 1938 follows and is called Shannon's Equation. |
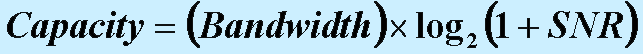 |
| SNR stands for Signal to Noise Ratio.
Obviously, the ability to discern a signal in a particular range of
frequencies influences the range's capacity. Notice that the
capacity increases as either the bandwidth and/or the SNR increases
as you'd expect. Now we work some examples. Example. Phone Line Capacity. A phone line normally has a bandwidth, in the more precise usage of the word, of 3000Hz. This is measured from 300 Hz to 3300 Hz. The standard SNR for a phone line is 3162. Based on this we get the following calculation. C = 3000log2(1 + 3162) = 3000log2(3163) = 3000(11.62) 34,860 bps ~ 34.86 Kbps Example. Wireless Channel Capacity. Since I don't really know the SNR of the wireless frequencies let's assume it is around the SNR of a phone line. Depending on the wireless standard, the channels have differing widths. Unfortunately, these channels usually overlap in some specifications such as the 802.11b. |
| Standard | Overlapping | Bandwidth | Capacity |
| 802.11b | Yes | 22 MHz | C = 22,000,000log2(1 + 3162) = 22,000,000(11.62) = 255,640,000 bps ~ 256 Mbps |
| 802.11a | No | 20 MHz | C = 20,000,000log2(1 + 3162) = 20,000,000(11.62) = 232,400,000 bps ~ 232 Mbps |
| 802.11g | No |
| So I know the SNR for wireless isn't this good!!!
Let's assume the numbers for SNR in Forouzan's book are actually in dB. Then a number of sources state that we want the following SNR for wireless channels. These sources also state that these SNRs need to be determined and assessed! |
| Quality | SNR |
| minimum | 20 dB |
| excellent | 40 dB |
| Thus the calculations change to the following. |
| Standard | Overlapping | Bandwidth | Capacity |
| 802.11b | Yes | 22 MHz | C = 22,000,000log2(1 + 40) = 22,000,000( ) = bps ~ Mbps |
| 802.11a | No | 20 MHz | C = 20,000,000log2(1 + 40) = 20,000,000( ) = bps ~ Mbps |
| 802.11g | No |
| These numbers still are not believable for a number of reasons. So I need to do more checking! |