Some Background on Number Systems

 

Introduction.  Modern computing is still based on bits of information.  They perform high speed calculations and operations using circuits based on information storage that can be conceptualized as 0s and 1s.  Thus the number system underlying computing is called a binary system or base 2 number system.  Binary code is sometimes referred to as machine language.

We are all familiar with the decimal system.  Numbering things like 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 and so on.  But remember learning Roman numerals,  I, II, III, IV, V, VI, VII, VIII, IX, X and so on?   Anyway, can you imagine trying to do multiplication or division in Roman numerals?  It's nasty!

The decimal system is considered by some sources to have come out of India through Islam.  Thus it is called the Hindu-Arabic system by some.  But as you might assume, since the decimal/Hindu-Arabic system came from Islam into Christianity it was considered to be the work of the devil by some!  Among other things, making use of the number zero was quite a problem for some people.  But without it, doing a lot of things becomes quite a bit more difficult.

Now, you poor computing students in the 21st century need to learn at least a little bit about some other number systems.  This is important since everything about implementing desires on computers must eventually be translated into binary.

The Decimal System.  Because you've likely forgotten you know this we are going to spend some time reviewing some of the basic logic of the decimal system.  This is the same as working in base 10.

Remember that the number 10,974 is spoken as ten thousand nine hundred and seventy four.  This could also be said as

1 unit of   10,000
0 units of  1,000
9 units of  100
7 units of  10
4 units of  1

So we actually read this from left to right, but when we build it we build it from right to left.

 

106 105 104 103 102 101 100
1,000,000 100,000 10,000 1,000 100 10 1
Number of each of these in 10,974
0 0 1 0 9 7 4

 

Notice that we can use any of 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 in any of the places but nothing else.  Notice there are ten digits that are so familiar you have probably never considered you could use anything else.

We won't review things like addition or multiplication algorithms.  But remember how important it was to do things like maintain particular places and carry digits.  So now that you have spent your life getting used to a 10 digit system we are going to review a two digit system and then a sixteen digit system.

The Binary System.  So how is it to do things like add, subtract or multiply if you have a binary system with only two digits to work with?  Now all you have is 0 and 1.  Let's just try to see what 10,974 looks like in binary.

 

  213 212 211 210 29 28 27 26 25 24 23 22 21 20
Decimal 8192 4096 2048 1024 512 256 128 64 32 16 8 4 2 1
Number of each of these in binary representation of decimal 10,974
  1 0 1 0 1 0 1 1 0 1 1 1 1 0

 

So

10,974 base 10 = 10101011011110 base 2

or

10,974 = 8192 + 2048 + 512 + 128 + 64 + 16 + 8 + 4 + 2

Fortunately for us all, we will not go into any great depth with respect to operating with the binary system.

But the idea behind using the binary system within computers is that you can use voltage levels or other characteristics of electrical signals to represent numbers.  Generally this is described as having the voltages on or off for a bit, but it really isn't exactly like this.  Then bits can be put together in sequences to represent larger numbers.  This is one of the reasons there is something called bytes which are usually 8 bits placed together.

But if all we used was one byte to represent a number, the largest number we could represent would be 511 base 10 = 11111111 base 2.  This is why things like integers usually require 4 bytes to represent, floating point numbers require 8 bytes and so on.  For example, if we use 4 bytes to represent an integer and ignore whether we can have positive or negative entries then the largest integer we could represent is

232 - 1 = 4,294,967,295

 

Which is quite a large integer, but not anywhere near the amount of money you hope to make each year as a junior computist.

The Hexadecimal System.  Now that you have endured a minimal number of the terrors of the binary system we are going to talk a bit about the hexadecimal system or base 16.  Since we have only 10 digits that we commonly use in the decimal system we run into problems trying to come up with 16 digits to use for a hexadecimal system.  Thus the single digits usually make use of letters so that the following correspondence exists.

 

Hexadecimal 0 1 2 3 4 5 6 7 8 9 a b c d e f
Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

 

So now we want to represent 10,974 in hexadecimal.

 

  165 164 163 162 161 160
Decimal 1,048,576 65,536 4096 256 16 1
Number of each of these in hexadecimal representation of decimal 10,974
  0 0 2 a d e

 

So

10,974 base 10 = 2ade base 16

or

10,974 = (2 x 4096) + (10 x 256) + (13 x 16) + 14

So you are likely to be asking where have you seen the hexadecimal system?

  • You are likely to have seen it when one or more magnificent Microsoft programs aborts and gives you a message about a problem at some address like 2a3d00e1.
  • When working with colors in HTML
    • For example, the background color for this page is bgcolor="#EDF4ED"

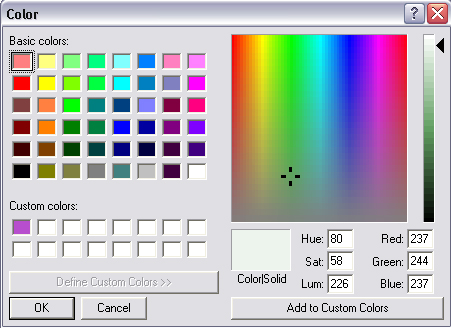
The bgcolor="#EDF4ED" looks like

 

 

in the color picker.  Whether you know it or not, there is a theory that all colors can be represented by a mixture of red, green and blue.  The numbers for this give the Color|Solid color for our background.

Red = 237     Green = 244     Blue = 237

which in hexadecimal is

Red = ED     Green = F4     Blue = ED

Now you can see where the bgcolor="#EDF4ED" comes from.

We could say a lot more about binary and hexadecimal systems, but this largely mimics what is done in the text with some augmentation.