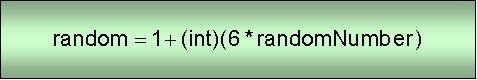
Random Rolls of a Die

 

Introduction.  In the last webpage we surveyed how random numbers can be generated and shifted to work for different ranges of equally likely values.  Now we need to determine how to simulate the rolling of a single die using random numbers.

A single die, in theory, is supposed to equally likely turn up with either a 1, 2, 3, 4, 5 or 6.  Notice how this is just somewhat different than what we did in the last webpage.  Being more specific we need random numbers that have the following characteristics.

  • equally likely to be something between 1 and 6
  • be an integer

So it might not surprise you that we can pretty much make use of what we did in the last webpage but cast the  results to an integer.  But you also need to remember that when you cast double to integers it truncates them downward.  So our function for for doing this will have to be the following.

 

 

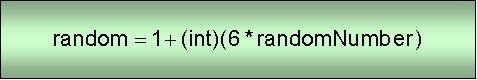
Everything is one higher than you'd expect from our formula in the last webpage because we are casting them to integers as we don't get zero on any rolls.  The lowest value we can get is one.

Our first application that will generate and display 20 random rolls of a die and should be called RandomRolls,java.

 

import javax.swing.JOptionPane;

public class RandomRolls
{

public static void main( String args[ ] )
{
int value, i;
String output = "";

for (i=1; i<=20; i++)
{

value = 1 + (int)(Math.random( )*6);
output = output + value + " ";

//  starts a new line every fifth number
if (i%5 == 0) output = output + "\n";

}

JOptionPane.showMessageDialog( null, output, "20 Random Numbers from 1 to 6",
JOptionPane.INFORMATION_MESSAGE );

System.exit(0);
}

}

 

When running this you should see something similar to the following output.  Hopefully, the program uses a different seed number, such as the current time, to initialize the random( ) generated sequence of numbers so you should see somewhat different numbers.

 

 

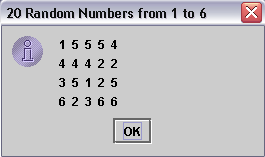
This program does the following

  • the first section of code
    • imports the swing.JOptionPane class
    • declares the overall inclusive class RandomRolls
  • within the method main( )
    • declares a counter
    • declares a double used for a place to return the random numbers
    • initializes a string used for output
    • develops a for loop block of code to
      • generate the random numbers using

      1 + (int)(Math.random( ) * 6)

       
      • adds these and a blank to the output string
      • puts these on a new line after every fifth entry
        • i % 5 == 0  whenever i is divisible by 5
    • displays the output using the showMessageDialog( ) method from the JOptionPane class in the swing package
    • then it ends the method main( )

Frequency of Rolls.  One of the ways that researchers try to validate the capability of an algorithm to generate the desired distribution of random numbers is to

  • create a distribution of numbers based on the algorithm
  • use statistics to validate

In this vein we will generate 24,000 rolls of a die and count up how many times we get a 1, 2, 3, 4, 5 and/or 6.  These results are done in the following application RollDieFrequency.java.

 

import javax.swing.*;

public class RollDieFrequency
{

public static void main( String args[ ] )
{

int frequency1 = 0, frequency2 = 0, frequency3 = 0,
frequency4 = 0, frequency5 = 0, frequency6 = 0,
roll, face;

for (roll=1; roll<=24000; roll++)
{

face = 1 + (int)(Math.random()*6);

switch (face)
{

case 1:

++frequency1;
break;

case 2:

++frequency2;
break;

case 3:

++frequency3;
break;

case 4:

++frequency4;
break;

case 5:

++frequency5;
break;

case 6:

++frequency6;
break;

}

}

JTextArea outputArea = new JTextArea(7,10);

outputArea.setText(
"Face\tFrequency" +
"\n1\t" + frequency1 +
"\n2\t" + frequency2 +
"\n3\t" + frequency3 +
"\n4\t" + frequency4 +
"\n5\t" + frequency5 +
"\n6\t" + frequency6 );

JOptionPane.showMessageDialog(null, outputArea, "Rolling a Die 24000 Times",
JOptionPane.INFORMATION_MESSAGE );
System.exit(0);

}

}

 

After running it you should see something like the following.

 

 

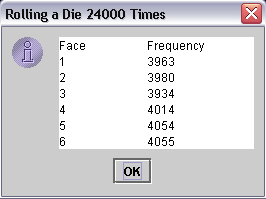
Notice how each value is relatively close to 4000, but none of them is exact.  How close should they be?  That's a very good question and outside the scope of this course.

The code can hopefully be better understood through the following outline.

  • the swing package is imported for input and output display
  • within the method main( )
    • initialize integer variables used to accumulate the frequency of each roll to 0
    • declare an integer to count how many times a die has been rolled = roll
    • declare an integer face to receive what the expression used to randomly generate the roll of a die evaluates to
    • develop a for loop that runs from 1 to 24000 to keep track of  the number of rolls
      • generate each roll using the function

face = 1 + (int)(Math.random( ) * 6)

    • develop a switch statement based on the face value
      • increment the frequency for that case
    • declare and initialize a textArea for the output
    • add the output to the textArea
      • \n for a new line for each outcome
      • \t to consistently space for each frequency
    • display the results using the showMessageDialog( ) method of the JOptionPane class
    • exit the program
  • end main( )
  • end the class RollDieFrequency

This is all we will say on this topic.

In the next webpage we will develop some code to simulate playing the game of craps.  You should make sure you know how to play the game before trying to understand the code.  There is some discussion of the rules before we dig into the code in the next webpage.