Sorting an Array with a Bubble Sort

 

Introduction.  Another classic problem in the computer sciences is sorting.  It is possible to think of plenty of applications of searching such as the following.
  • organizing grades for a course in descending order by their overall score
  • organizing clients by the amount of money they've spent with your firm
  • ordering potential students to be considered for financial aid by their total SAT score
  • finding the physicians on your sales call list that you haven't visited and order them by how long it has been since you have visited
  •  

Obviously, these sorts of scenarios are endless.

So, you should be able to see that quickly and efficiently being able to find the desired information is very important.  If it takes too long then it delays all kinds of other things that may be more important.

This next applet will randomly generate an array of size 10 of integers from 1 to 100.  Then this array will be sorted in ascending order.

We will use an approach called a bubble sort because of how numbers bubble to the top of the list.  Rather than discuss this in the abstract we will

  1. first develop the code
  2. run the program
  3. examine the output
    1. discuss the steps that are taken to sort the array
  4. discuss the code

I think it will be much easier to discuss the code after seeing an example and describing the bubble sort process in words.

This applet is a modification of one of the same name in Deitel and Deitel.  The major modification is to display the intermediate steps in the sorting process so we can discuss them.  The program should be called BubbleSort.java.

 

import java.awt.*;
import javax.swing.*;

public class BubbleSort extends JApplet
{
String output = "Data items in original order\n";
int a[];

public void init()
{
JTextArea outputArea = new JTextArea();
Container c = getContentPane();

c.add(outputArea);

a = new int[10];
// randomly generate an array of 10 integers
// between 1 and 100 to be sorted
for (int i = 0; i < a.length; i++)
a[i] = 1 + (int) (Math.random() * 100);

// display the original ordering of the array
for (int i=0; i < a.length; i++)
output = output + " " + a[i];

bubblesort( a );

// display the final ordering after bubble sort is completed
output = output + "\n\nData items in ascending order\n";
for (int i=0; i < a.length; i++)
output = output + " " + a[i];

outputArea.setText(output);
}

// sort the elements of an array with a bubble sort
public void bubblesort( int b[] )
{
int passThrough;
// loop for number of times to pass through array
for (int pass = 0; pass < b.length; pass++)
{
// loop to actually pass through the array
// and swap adjacent pairs of numbers if appropriate
for (int i=0; i < b.length - 1; i++)
// swap if i-th entry is greater than i+1-st entry
if (b[i] > b[i+1])
swap(b, i, i+1);

// section of code to display the results
// of the sort after each pass
passThrough = pass + 1;
output = output + "\n\nOrder after pass " + passThrough + "\n";
for (int i=0; i < b.length; i++)
output = output + " " + b[i];
}
}

// swap two elements of an array
public void swap( int c[], int first, int second)
{
int hold;

hold = c[first];
c[first] = c[second];
c[second] = hold;
}
}

 

Notice, we have done a fairly minimal implementation with no error trapping and a flow layout.  Since the size of the applet window impacts the display it is given below in BubbleSort.html.

 

<html>
<applet code="BubbleSort.class" width=220 height=600>
</applet>
</html>

 

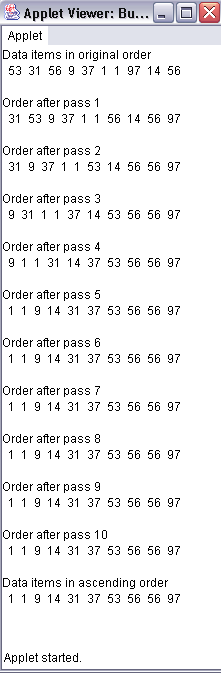
I ran the program to generate the following display for our discussion.  But your results will almost surely differ due to the random number generation.  Fortunately, you should be able to understand some basic operating principles in the code before examining it.

 

 

 

Notice the initial array of randomly generated integers from 1 to 100 is

53  31  56  9  37  1  1  97  14  56

Notice how we actually have some recurrences of numbers in this small array.  What this implies about random number generation is beyond the scope of this course.

Take some time to think how you would want to sort these in order from lowest to highest and remember you need to write code to do it.

A bubble sort works on the basic principle of

  • looking at an adjacent pair of numbers

    • if the first number in the pair is higher than the second then swap them

    • if the first number in the pair is not higher then leave their order as is

  • then move to the next pair, but make use of whatever the current last number is in your current pair

    • don't skip past the number that is highest in your previous pair

    • make use of it to compare to the next number after

Describing this in more detail, let's talk about how this array was sorted.  This sequence of steps as a whole will be called a pass through the array.

  1. the first pair is 53 and 31

    • 53 is greater than 31 so swap them

    • the array changes to

    • 31  53  56  9  37  1  1  97  14  56

  2. the second pair is now 53 and 56

    • 56 is greater than 53 so don't swap them

    • the array stays the same at

      • 31  53  56  9  37  1  1  97  14  56

  3. the third pair is now 56 and 9

    • 56 is greater than 9 so swap them

    • the array changes to

      • 31  53  9  56  37  1  1  97  14  56

  4. the fourth pair is now 56 and 37

    • 56 is greater than 37 so swap them

    • the array changes to

      • 31  53  9  37  56  1  1  97  14  56

  5. the fifth pair is now 56 and 1

    • 56 is greater than 1 so swap them

    • the array changes to

      • 31  53  9  37  1  56  1  97  14  56

  6. the sixth pair is now 56 and 1

    • 56 is greater than 1 so swap them

    • the array changes to

      • 31  53  9  37  1  1  56  97  14  56

  7. the seventh pair is now 56 and 97

    • 56 is less than than 97 so don't swap them

    • the array stays the same at

      • 31  53  9  37  1  1  56  97  14  56

  8. the eighth pair is now 97 and 14

    • 97 is greater than than 14 so swap them

    • the array stays the same at

      • 31  53  9  37  1  1  56  14  97  56

  9. the ninth pair is now 97 and 56

    • 97 is greater than than 56 so swap them

    • the array stays the same at

      • 31  53  9  37  1  1  56  14  56  97

Notice how this corresponds to the list that appears in the applet window after the first pass.  You should also notice

  • how the highest number in the list has bubbled up to the end and will no longer move

  • how all the larger numbers were swapped and moved towards the end until the encountered an even higher number

This is why this is called a bubble sort.  The higher numbers sort of bubble up.  the lower numbers sort of bubble down.

The second pass will work similarly.  I won't present it, but you should notice how the next highest number bubbles up to the second to the last entry and how some other numbers bubble up and others bubble down in the swap.

You should also be able to see that we need to take as many passes as there are elements in the array in order to make certain everything has bubbled to the correct relative position.

Code Discussion.  We will use our usual outline form to discuss the code.

  • import java.awt.*
  • import javax.swing.*
  • declare the overall inclusive class BubbleSort
    • extending JApplet
  • declare and initialize a string for output
  • declare an integer array a[ ] to contain a randomly generated set of integers

     

  • declare method init( )
    • declare a JTextArea called outputArea for output
    • declare a container to be the content pane of the applet window
    • add the JTextArea outputArea to the container
    • declare an array a[10] of integers
    • add the JTextField to the container
    • use a for loop to fill the array a[ ] with randomly generated integers from 1 to 100
      • a[i] = 1 + (int) (Math.random( ) * 100)
    • use a for loop to display the a[ ] array before sorting
      • add each element of the array to the output string while putting a space between each entry
    • invoke the bubblesort( ) method on a[ ], the array of randomly generated integers
      • bubblesort will display the results of the intermediate passes
    • add a string to the output that tells the user that they are about to see the final sorted array
    • use a for loop to display the a[ ] array after sorting
      • add each element of the array to the output string while putting a space between each entry
    • set the output string as the text within the outputArea
  • end the method init( )

 

  • declare method bubblesort( )
    • returns nothing since the swap operations are on the original array that is passed by reference to its memory address
    • requires the array a[ ] of randomly generated integers be passed but they are called b[ ] locally
    • declares an passThrough counter as san integer to be used locally for display purposes
    • uses a for loop to make a number of passes through the array that equals the size of the array
      • uses a for loop to go through the entire array to examine each consecutive adjacent pair of values
        • invokes swap( ) method if first number in the pair is greater than the second number in the pair
        • loops to next pair
      • adds a little header to the output string to let the user know which pass is about to be displayed
      • use a for loop to display the b[ ] array after sorting
        • add each element of the array to the output string while putting a space between each entry
  • end the method bubblesort( )

 

  • declare method swap( )
    • returns nothing since the swap operations are on the original array that is passed by reference to its memory address
    • requires the array of random numbers be passed to it but gives them a new name c[ ] to be used locally even though it modifies the original array a[ ]
    • requires the index number of the first entry in the array to be swapped to be passed
    • requires the index number of the second entry in the array to be swapped to be passed
    • declares an integer called hold to temporarily hold onto the value to be swapped so it doesn't get lost
      • takes the value of the first entry in the current pair and assigns it to the hold value
      • assigns the second value (the lower value) in the pair to where the first one was
      • assigns the hold value to the second array element in the pair
    • ends the swap( ) method

 

You can play with this all you want.