Measuring Validity for Moving Average Forecasts

 

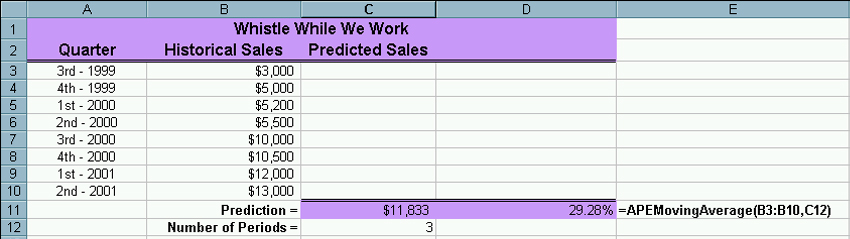
Introduction.  Again we are going to work at developing more objective measures for the quality of a forecast.  We are again going to focus on APE = Average Percentage Error.  Due to some previous familiarity I will start by showing the spreadsheet computations for APE for the two-period and three-period moving average forecasts we did on the Whistle While We Work data.

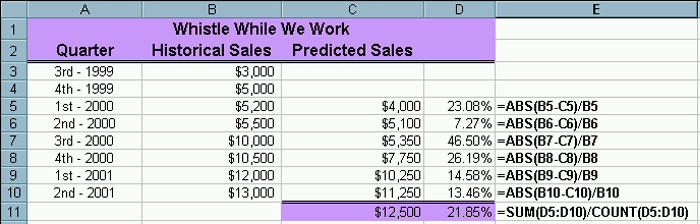
The spreadsheet for the two-period moving average is below.

 

 

Notice that the average error is about 21.85%, which is up from many of the error estimates we got for exponential smoothing.  Though none of these approaches is giving a very good forecast.

The spreadsheet for the three-period moving average forecast is next.

 

 

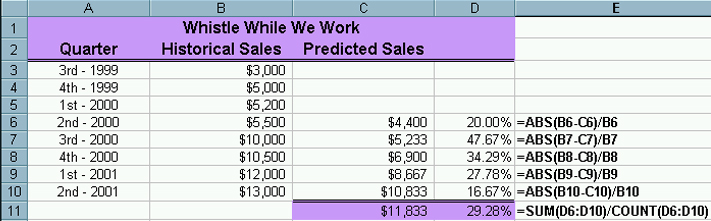
Notice that this error is actually worse than that for the two-period.  This shouldn't be too surprising because the major thing going on in this data is a trend and we have yet to study any forecasting methods that work well for trends!

But we need to arrive at some general statements about computing our error terms and computing their averages.

  • If there are n periods of historical data
  • and we are doing an m-period moving average forecast

there will be

  • n - m periods for making comparisons between past observations and "past predictions"
  • we need m periods of data for each forecast
  • there are m blank periods that correspond to our earliest historical data where it wasn't possible to make any predictions. 

These all influence the nature of our loops when we compute past predictions and errors.

The code for computing the APEMovingAverage function follows.

Function APEMovingAverage(Historical, NumberOfPeriods) As Single
' Declaring and initializing variables
Dim Item As Variant
Dim Counter As Integer
Dim Accumulation As Single
Dim NumberOfPredictions As Integer
Dim ErrorCounter As Integer
Dim ErrorPercentage As Single
Dim ErrorAccumulation As Single
Dim PredictionCounter As Integer
Dim HistoricalSize As Integer
Dim Prediction(100) As Single

' Initializing variables
Counter = 1

Accumulation = 0#

 ' Determining the size of Historical array
HistoricalSize = Historical.Count

' We can determine the number of predictions and comparisons we can perform
NumberOfPredictions = HistoricalSize - NumberOfPeriods

For PredictionCounter = 1 To HistoricalSize - NumberOfPeriods

For Counter = 1 To NumberOfPeriods

' Accumulating the appropriate number of most recent previously observed values

Accumulation = Accumulation + Historical(PredictionCounter + Counter - 1)

Next Counter

Prediction(PredictionCounter) = Accumulation / NumberOfPeriods
Accumulation = 0#

Next PredictionCounter

' Determining the errors

For ErrorCounter = 1 To HistoricalSize - NumberOfPeriods

ErrorPercentage = Abs(Historical(ErrorCounter + NumberOfPeriods) - _
Prediction(ErrorCounter)) / Historical(ErrorCounter + NumberOfPeriods)

ErrorAccumulation = ErrorAccumulation + ErrorPercentage

Next ErrorCounter

APEMovingAverage = ErrorAccumulation / (HistoricalSize - NumberOfPeriods)

End Function

The code will be discussed in class.

You want to check this function on your spreadsheet against other things we've developed.  Make sure you choose the number of periods in the moving average the same for both the prediction and the error computation.  For the WWWW three period moving average the spreadsheet follows.