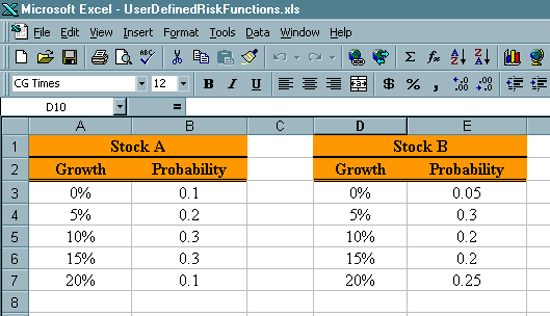
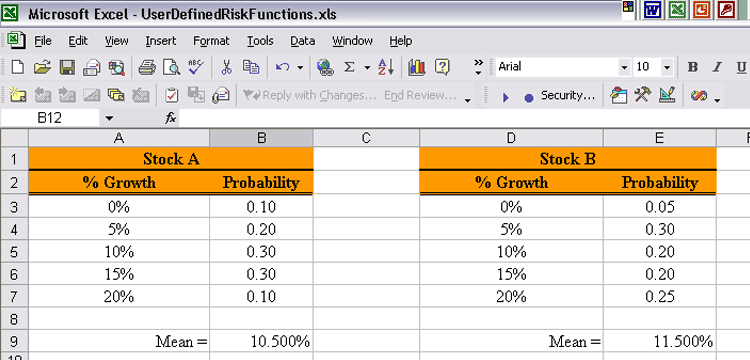
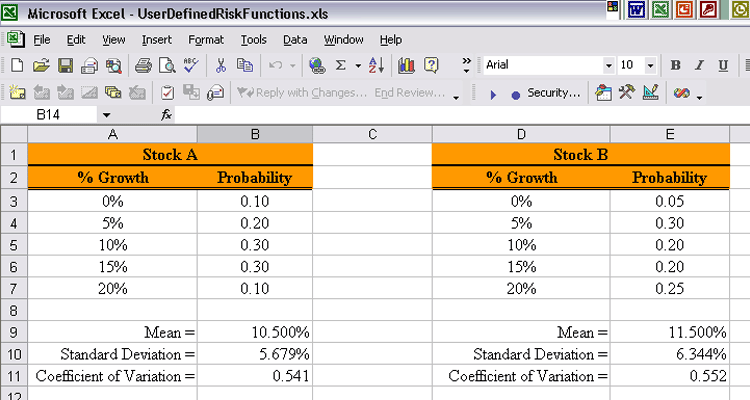
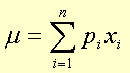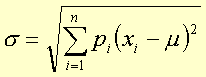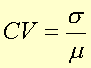| How can we compare the gains we might expect to see
for these stocks given this new way of presenting the information?
We can think of this new codification as a discrete distribution. The percentage rate of return is the random variable. The entries in each of the Growth columns is the potential values of the random variable. The entries in the Probability column are the probabilities that the growth will be the corresponding value in the Growth column. But as is always the case it is difficult, if not nearly impossible to compare entire distributions. Comparisons are more successful if they are done between single numbers. Again we will work with expectations. We will again want to use the mean, standard deviation and coefficient of variation. But Excel does not have any built in functions for these performance measures when we are working with distributions. The functions we used in the previous webpages related to sample expectations. The first thing we need to do is refer to a Statistics text to find the formulas for these expectations when we are working with distributions. Then we will need to develop our own functions for computing these performance measures. Expectations for Discrete Distributions. What we are working with in this situation are called discrete distributions. We will now present the formulas for our desired expectations for discrete distributions.
The distribution mean is
The distribution standard deviation is
The distribution coefficient of variation is
|