Assessing Long Term Stock Risk Using Excel

 

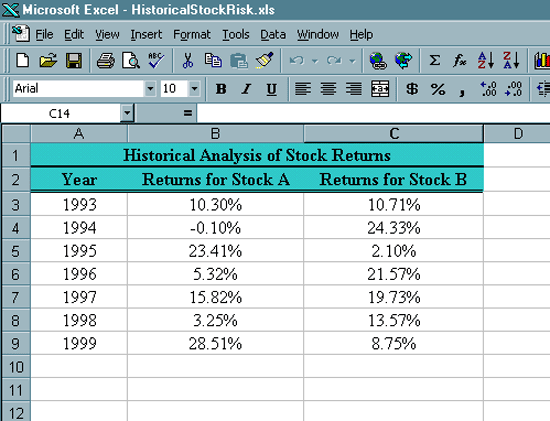
Introduction.  Let's assume you have a couple thousand dollars and you are looking to purchase stock in at least a couple different corporations.  You are expecting to hold onto this stock for a fairly long time.  You are not a day trader.  You know a fair amount about two different companies based on past experience and you are curious about their stock performance.  The first step is to collect some information on the annual percentage gains for two different stocks over the last several years.  

The desired information is contained in the following table.

 

Year Returns for Stock A Returns for Stock B
1993 10.30% 10.71%
1994 -0.10% 24.33%
1995 23.41% 2.10%
1996 5.32% 21.57%
1997 15.82% 19.73%
1998 3.25% 13.57%
1999 28.51% 8.75%

 

Notice that both of these stocks have had some very good years along with some off years.  You are likely to want to find some sort of average rate of return, but you are also going to be concerned with the variation in returns.

Now you want to start by typing some text into the cells.  We will modify the formats of most of these cells later.

  1. Type Historical Analysis of Stock Returns in cell A1

  2. Type Year in cell B2

  3. Type Returns for Stock A in C2.

  4. Type Returns for Stock B in D2.

  5. Now you should adjust the column widths so that all of the letters fit inside each cell and center the column headers.

  6. You should also format the cells to give them some color pattern for the background and put some border lines in to help make the spreadsheet easier to view.

  7. In cell A3 you want to type 1993 and center it.  Now you want to fill in the rest of the years using the Fill feature in Excel.

  8. Highlight cells A3 ... A9 and select the Edit menu.

  9. Select the Fill item on the menu and then the Series item on the submenu that appears.

  10. Select the Columns option button, select the Linear Type and make sure the step size is 1.

  11. Click on the OK button and Excel will fill in the years.

  12. Format the cells B3 ... C9 to align the entries in the center and display percentages with two decimal places.

At this point your spreadsheet should look like the following.

 

Computing Expectations.  The word expectations has considerable statistical meaning in addition to its typical usage.  We will compute measures that are averages of the values or averages of the dispersion or some ratios of these measures.  Expectations are used to give single measures that somehow represent the data they are derived from.  It is not easy to make decisions based on an entire distribution, but it is much easier to describe expectations about the mean or dispersion.  While a decision maker definitely loses information by creating these expectations they still provide a lot of usefulness.

The first expectation we will work with is called the mean.  This should be quite familiar. The definition of a sample mean is

where

  

is the sample.

But as you can see the mean is not a perfect representation of the overall distribution.  For example, using the average height  and size of everyone to make clothes all the same size would not be very effective.  Yet by the same token the mean does give some information about the distribution of data, at least a general sense of its center of gravity.

Another feature of a distribution of data is the extent to which it is spread out.  There are several measures that are typically used to represent this, such as the range and variance.  We will focus on the standard deviation since this has the same units as the data.  The definition of the sample standard deviation for the same sample as above is

Now you should compute the mean and standard deviation for the stock data.

  1. In cell A10 type Mean =   and right justify it.

  2. In cell A11 type Standard Deviation =   and right justify it.

  3. In cell B10 type   =AVERAGE(B3:B9)

  4. In cell B11 type  =STDEV(B3:B9)

  5. Copy B10:B11 to C10:C11.

Now the spreadsheet should look like the following.

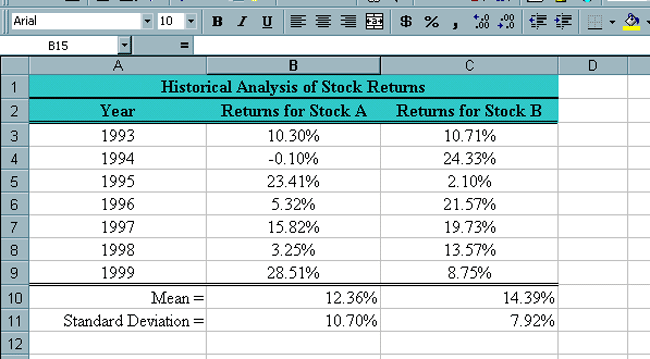
Notice that they each have different means and standard deviations.  In this case Stock B does better with both measures.  This is seldom the case.

The greater the standard deviation of such returns the greater the risk of investing in the stock.

There is one other measure we want to consider called the coefficient of variation.  It is often the case that something with a larger mean will also have a larger standard deviation.  Consider

  • the lengths of the pencils in this classroom
  • the heights of the people in this classroom

If you were going to try and compare the variation between them you would find that the standard deviation of the heights of the people is much greater than the standard deviations  of the lengths of the pencils.  But sometimes it is important to try to compare the amount of variation between seemingly disparate things such as the price of Microsoft and the price of an IPO.  They are almost surely going to appear on very different scales.  But if we divide the standard deviation associated with each of the stocks by their respective means we are much more likely to get a ratio that we can compare.

The sample coefficient of variation is defined as

Excel does not have  built in function for CV, but we can easily compute them with the following steps.

  1. Type Coefficient of Variation =  in cell A12.
  2. Type  =B11/B10  in cell B12.
  3. Copy the formula in B12 to C12.

You should now have a spreadsheet like the following.

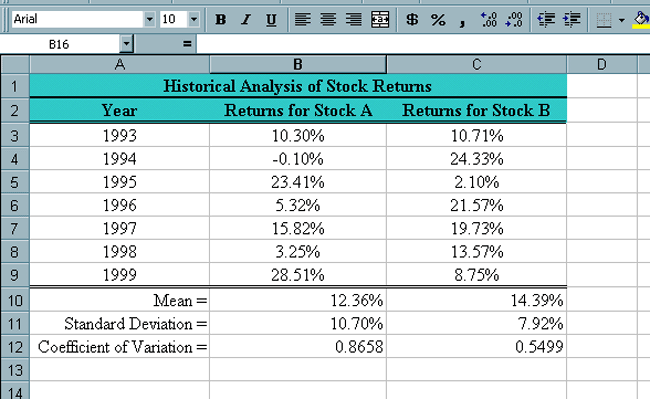
Notice that the coefficient of variation for Stock B is also better.

At present it might appear that you should put all of your money into Stock B since it has the higher mean growth rate and the lower standard deviation.  In spite of this there are reasons for continuing to consider purchasing quantities of both stocks.  In the next web page we will use Excel to investigate putting stocks together into a portfolio to improve returns and decrease risk.