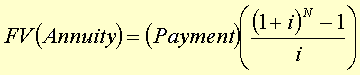
Annuities
|
Some Background. We have already talked about mortgages and by analogy, car loans. We started with these because you are likely to have some familiarity with them. One of the main features that each of these loans have is the payment of a particular amount of money to a lender over a period of time. The money is paid at equal time intervals, usually months. The amount of money in each payment is nominally the same at each point in time. At some point in time in the future you will have paid off the loan. Mayes & Shank state that annuities are a series of nominally equal cash flows, equally spaced in time. Thus car payments are an annuity, so is a mortgage. If you are paying money each month into a retirement account this is likely to be an annuity. Or maybe your parents saved money for your college expenses using an annuity. The length of time between payments is usually one month, though this isn't necessarily the length of time between payments. In this webpage I will present some background about annuities and then in the next webpage we will develop a UserForm that will allow a user to determine several different things about annuities based on particular inputs. The Future Value of an Annuity. Let's assume you start putting money into an annuity at the time your child is about 3 years old. You know you will want the money to be available in about 15 years, though you will not use all of the money all at once and you may well still pay into the annuity until your child is finished with school. If you pay $200 each month into an investment account that states you will get 10% annually on your money, how much will you have in 15 years? Answering this question is equivalent to determining the future value of your annuity. I don't want to get involved in the derivation of the following equation, but if anyone wants to see it I will be more than happy to work through it for them. |
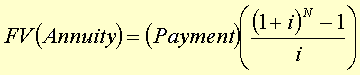
where
If there are m payments to be made each year you should divide each interest rate by m and multiply the number of years by m. In our situation the formula becomes |
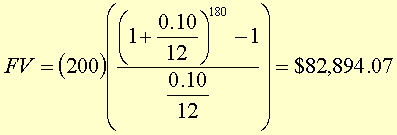
| You can see that this nets you quite a bit of
money.
A Pattern When Using Formulas. Whether or not you've noticed it, there is an important pattern involved in almost every class where you make use of formulas. When I went through most of my year of Physics classes in college I was not what anyone would consider to be real motivated. For example, I couldn't have discussed even the tiniest bit about how electrons are supposed to move through fields. But I noticed something important when preparing for tests. Even though I had to know Calculus to get through my Physics classes the basic substance of what I needed to know in order to get through my tests could be broken down to a few things and a process.
What does it mean to solve for the unknown? Maybe this is best illustrated by using annuities. Consider the formula above for the FV of an annuity. There are four variables in the formula, FV, Payment, N and i. Theoretically, at any given point in time you could use this formula to determine one of the variables given you have values for the other three. While this is often easier said than done, it is the basis of solving for the unknown. The following table illustrates this further. |
| Unknown | Knowns | Formula | Excel Function |
| FV = Future Value | Payment, N, i | 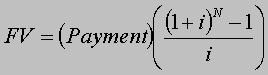 |
=FV |
| Payment | FV, N, i |
|
=PMT |
| N = Number of Payments | FV, Payment, i |
|
=NPER |
| i = Interest Rate | FV, Payment, N |
No closed form solution exists, needs a numerical method |
=RATE |
| It is unimportant to know these formulas for this
class, they are included to illustrate my point. It is possible
that you are completely unfamiliar with the ln( ) function, the inverse
function of exponentiation with a particular base. This is not the
least bit important in this class. Notice that each of these
scenarios has a built in Excel function which will give us the desired
solution.
More About the Excel Annuity Functions. Ultimately, our goal is going to be to create a user friendly form that will make the computation of the solutions of these annuity related questions relatively effortless for the user. We will focus specifically on that issue in the next webpage. Currently I want to include more discussion about the built-in Excel functions. The following four tables contain a discussion of each of the functions and the inputs. Inputs in bold letters are required. |
| = FV( i, N, Payment, PV, Type ) | |
| Input |
Description |
| i = Interest Rate | This is the per payment period interest
rate.
It is often the annual rate divided by 12 if the payments are monthly. |
| N = Number of Payments | This is the total number of payments.
It is often the number of years times 12 if the payments are monthly. |
| - Payment | You must enter the negative of the per period payment amount. |
| PV | The present value of the annuity which is assumed to be 0 if omitted. |
| Type | 0 = payment at end of period (default) 1 = payment at beginning of period |
| = PMT( i, N, PV, FV, Type ) | |
| Input |
Description |
| i = Interest Rate | This is the per payment period interest
rate.
It is often the annual rate divided by 12 if the payments are monthly. |
| N = Number of Payments | This is the total number of payments.
It is often the number of years times 12 if the payments are monthly. |
| PV | The present value of the annuity. |
| FV | The future value or cash amount you want to attain when completes. This is assumed to be 0 if omitted. |
| Type | 0 = payment at end of period (default) 1 = payment at beginning of period |
| = NPER( i, Payment, PV, FV, Type ) | |
| Input |
Description |
| i = Interest Rate | This is the per payment period interest
rate.
It is often the annual rate divided by 12 if the payments are monthly. |
| - Payment | You must enter the negative of the per period payment amount. |
| PV | The present value of the annuity. |
| FV | The future value or cash amount you want to attain when completes. This is assumed to be 0 if omitted. |
| Type | 0 = payment at end of period (default) 1 = payment at beginning of period |
| = RATE( N, Payment, PV, FV, Type, Guess ) | |
| Input |
Description |
| N = Number of Payments | This is the total number of payments.
It is often the number of years times 12 if the payments are monthly. |
| Payment | |
| PV | The present value of the annuity. |
| FV | The future value or cash amount you want to attain when completes. This is assumed to be 0 if omitted. |
| Type | 0 = payment at end of period (default) 1 = payment at beginning of period |
| Guess | Ordinarily this is omitted, but you can put in something like 0.10 if 10% is a reasonable guess. |
| Now we will develop a UserForm that will allow a user to input certain values for an annuity and calculate what is unknown. This will be developed in the next webpage. |